Sorting is an everyday tool for programmers.We need to sort many things for many reasons.Like sorting to age,price etc.So there are many sorting algorithms like Merge Sort , Quick Sort, Bubble sort etc.

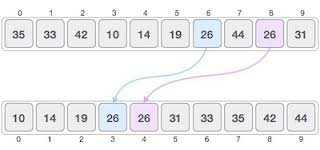
Stable & Unstable Sorting

If Two elements in array has same value, After sorting two things can happen.

1. They exchange their relative position.
2. They don't exchange their relative position.

From this example we can see that two '26' doesn't replace their relative positions.Hence it is stable sorting algorithms. Merge Sort ,Bubble Sort, insertion sort are actually stable sorting algorithm. On the other hand,Heap Sort, Quick Sort etc are unstable sorting algorithms.

Bubble Sort

Bubble Sort is the simplest algorithm. This is named Bubble Sort because its element just swap one by one. It doesn't have any special use in sorting.It is actually used for educational purposes to introduces sorting algorithms. I'm actually sorry if I disappointed you. Sort your emotions then.

Suppose we have an array of 3 numbers [3,6,2] which should be sorted in incrementing order. We can use Bubble Sort Algorithms to do so.
• At first, we have to take the first element of the array and compare it to the rest of the elements.If we get any elements lower than it, we will swap the position. Comparison 1: 3 > 6 ->NO
• Comparison 2: 3 > 2 ->YES swap the positions Then the array will be [2,6,3]
• Comparison 3: 6>3 -> YES swap the positions Then the array will be [2,3,6]

Bubble Sort Function

void bubbleSort(int array[], int length){

    for(int i = 0; i < length-1; i++){
        for(int j = i+1; j < length-1; j++){
            //first loop is used to check to the (length-1)th index of the aray
            //second loop is used to check the following items of the arrays
            int temp;
            if(array[i]<array[j]){
                temp = array[i];
                array[i]=array[j];
                array[j]=temp;
        }
    }
 }

Complete Program In Java

public class Main {
  static int array[] = {2, 1, 6, 5, 4};


    public static void main(String[] args) {

        int length = array.length;
        System.out.println("Unsorted Array");

        for (int i = 0; i < length; i++) {
            System.out.println(array[i]);
        }
        
        System.out.println("Unsorted Array");
        bubbleSort(array, length);
    }

    public static void bubbleSort(int array[], int length) {

        for (int i = 0; i < length - 1; i++) {
            for (int j = i + 1; j < length ; j++) {
                //first loop is used to check to the (length-1)th index of the aray
                //second loop is used to check the following items of the arrays
                int temp;
                if (array[i] > array[j]) {
                    temp = array[i];
                    array[i] = array[j];
                    array[j] = temp;
                }
            }
        }
        //for printing

        for (int i = 0; i < length; i++) {
            System.out.println(array[i]);
        }
    }
}

Time Complexity

Now talk about the time complexity of this algorithm.From the coding algorithm that is clear that we have to use a loop and a nested loop. So the complexity becomes O(n*n).

Now, let's see the time complexity of bubble sort in the best case, average case, and worst case. We will also see the space complexity of bubble sort.

• Best Case Complexity - This case occurs when no sorting is needed, i.e. the array is already sorted. The best-case time complexity of bubble sort is O(n).
• Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of bubble sort is O(n^2).
• Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of bubble sort is O(n^2).

Space Complexity

Here Space complexity is O(1). We just have to make a temp variable which is updated throughout the loop and doesn't need to create anything new.

Bubble short is majorly used where -

• complexity does not matter
• simple and shortcode is preferred

Now, let's discuss the optimized bubble sort algorithm.

Optimized Bubble sort Algorithm

In the bubble sort algorithm, comparisons are made even when the array is already sorted. Because of that, the execution time increases.

To solve it, we can use an extra variable swapped. It is set to true if swapping requires; otherwise, it is set to false.

It will be helpful, as suppose after an iteration, if there is no swapping required, the value of variable swapped will be false. It means that the elements are already sorted, and no further iterations are required. This method will reduce the execution time and also optimizes the bubble sort.

Program for optimized implementation of bubble sort in Java.

public class Bubble { static void print(int a[]) // function to print array elements { int n = a.length; int i; for (i = 0; i < n; i++) { System.out.print(a[i] + " "); } }

static void bubbleSort(int a[]) // function to implement bubble sort
{
    int n = a.length;
    int i, j, temp;
    for (i = 0; i < n; i++) {
        for (j = i + 1; j < n; j++) {
            if (a[j] < a[i]) {
                temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
        }
    }
}

public static void main(String[] args) {
    int a[] = { 35, 10, 31, 11, 26 };
    Bubble b1 = new Bubble();
    System.out.println("Before sorting array elements are - ");
    b1.print(a);
    b1.bubbleSort(a);
    System.out.println();
    System.out.println("After sorting array elements are - ");
    b1.print(a);
}

}

## Usage:-
- Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm. 
- In computer graphics it is popular for its capability to detect a very small error (like swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n). For example, it is used in a polygon filling algorithm, where bounding lines are sorted by their x coordinate at a specific scan line (a line parallel to x axis) and with incrementing y their order changes (two elements are swapped) only at intersections of two lines