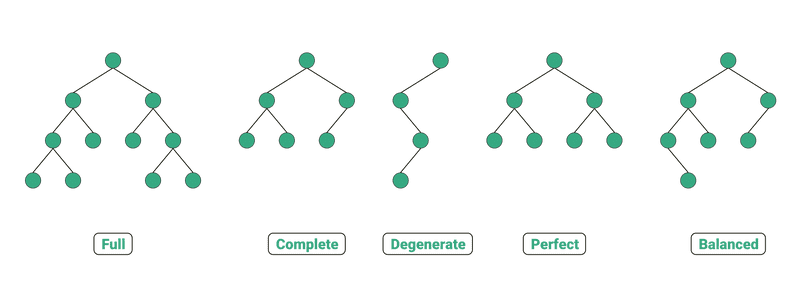Tree is a non-linear data structure which organises data in hierarchical form and is recursive in nature. It is a popular data structure used in wide range of applications. Every element is considered as a node which has a predecessor and a successor. Trees are further classified into many types I.e, Binary Tree, Complete Binary Tree, Perfect Binary Tree etc.

Structure of Tree

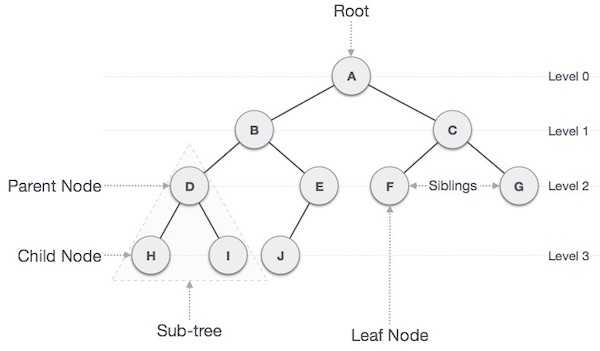
Structure of this Data Structure is clearly mentioned by its name which is in the form of a Tree. Every circle here represents a node. Let’s understand them better with the help of the diagram below

Root - Initial node of a tree , which divides the tree into n numbers.

Parent Node - The Predecessor of every node is its parent node. As D here is the parent of H & I.

Child Node - The successor of every node is its child node. Here, H & I are the successors of D.

Siblings - Nodes at the same levels are considered as siblings.

Leaf nodes - The nodes having no successors are the one’s which are considered as leaves.

Right Sub-tree - Nodes at the right side of the root node are the one’s of right sub-tree.

Left Sub-tree - Nodes at the left side of the root node are the one’s of left sub tree.

Types of Trees

Their are in basic 4 types of Trees

• Binary tree
• Binary Search tree
• AVL tree
• B-tree

Binary Tree

Binary tree is the one whose every parent node has atmost 2 children. Number of child nodes can be either 0,1 or 2. Binary Trees can further be classified into more types given below in the diagram.

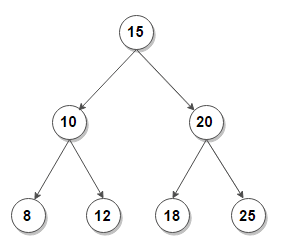
Binary Search Tree

BST is a lot similar to a binary tree in which every parent node has at most 2 children. Other than that, BST follows few properties which makes it different from a binary tree.

The properties are -

• Value in all the nodes of a left subtree should be lesser than the value in the root node.
• Value in all the nodes of a right subtree should be larger than the value in the root node.

The pictorial representation of BST is

AVL Tree

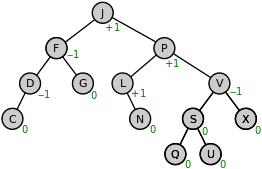
AVL trees are considered as the variants of binary tree which have the characteristics of both Binary tree and Binary search tree. These trees are self-balanced which means the height of left sub tree and right are sub tree are equal. This balanced is measured in terms of balancing factor.

Now, let’s understand what is a balancing factor -

• It is the difference between the left sub tree and right sub tree.
• The value of balancing factor must be 0 , -1 and 1 , which means each node will be having a balancing factor of 0,1 and -1.
• Values of nodes other than -1, to 1 in an AVL tree will represent an unbalanced tree that needs to be balanced.
• If a node has a balance factor of 1, it means that the left subtree is one level higher than the right subtree.
• If a node has a balance factor of 0, it means that the height of the left subtree and the right subtree is equal.
• If a node has a balance factor of -1, it means that the right subtree is one level higher than the left subtree or the left subtree is one level lower than the right subtree.

B-Tree

It is also known as height-balanced m way tree, where m is the order of the tree. B-tree is more generalised form of a binary search tree.  In the case of a binary tree, the leaf nodes might not be at the same level. However, in the case of a B Tree, all the leaf nodes should be at the same level. 

Properties of B-Tree are -

• The root may have between 2 and m children.
• All other nodes must have between [M/2] and m children.
• A node that has k children will have k-1 key values.
• Thus, the root may have only 2 children; all other nodes must be at least half full .

Traversals in Trees

Tree traversals means traversing or visiting each node of the tree. Other than tree data structure, Stack , Queue and Linked List only have one way for traversing which makes Trees different from them also.

Traversals are of 3 types

1. In-order Traversal - This traversal calls for the sequence of LEFT, ROOT, RIGHT.
2. Pre-order Traversal - This traversal calls for the sequence of ROOT ,LEFT, RIGHT.
3. Post-order Traversal - This traversal calls for the sequence of LEFT, RIGHT, ROOT.

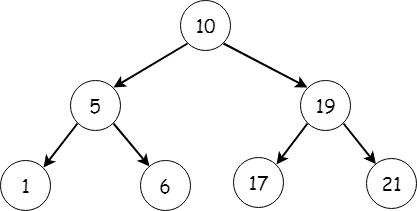
Now let’s understand these a help of an example

Taking the above tree into consideration let's understand how traversing is done

In-order Traversal (LEFT , ROOT, RIGHT) - Traverse the left sub-tree , visit the root , traverse the right sub-tree which makes the sequence (1,5,6,10,17,19,21)

Pre-order traversal (ROOT, LEFT , RIGHT) - Visit the root , Traverse the left sub tree , Traverse the right sub tree which makes the sequence (10,5,1,6,19,17,21)

Post-order traversal (LEFT,RIGHT,ROOT) - Traverse the left sub tree , Traverse the right sub-tree , visit the root which makes the sequence (1,6,5,17,21,19,10)